潘银萍
(西安交通工程学院机械与电气工程学院,陕西 西安 710330)
随着社会经济的发展、城市规模的扩大,为了提高城市交通运营水平、更好地解决交通堵塞问题和民众出行困难问题[1-2],许多大中型城市纷纷选择将城市轨道交通作为城市公共交通的重要组成部分。以地铁为“骨架”,以公交车、出租车为“毛细血管”的公交网络将成为城市公共交通的主要运营方式[3-5]。城市轨道交通具有运送量大、速度快、污染少等优势,其作用越重要,一旦发生故障或事故的后果也越严重。交通事故不仅严重影响市民的正常出行,还会造成生命和财产的重大损失。因此,人们对轨道交通系统可靠性和安全性的要求也越来越高。为了防止和减少事故、保证车辆正常运行[6-7],对轨道车辆的牵引系统进行可靠性分析、确定牵引系统的薄弱环节,对地铁车辆的可靠性设计以及车辆维修具有重要意义[8-9]。
本文结合某地铁线路的现场车辆检修记录,采用系统可靠性理论分析牵引系统的可靠性。首先,本文根据现场检修数据建立地铁牵引系统的故障模型,并对所建立的故障模型进行定性、定量分析。其次,本文对地铁牵引系统进行可靠性仿真。最后,本文确定了牵引系统的薄弱环节和各部件的重要度。
1.1 牵引系统简介
牵引系统是地铁车辆可靠运行的关键电气系统,一旦发生问题,地铁动力来源会受到影响,将使得列车牵引制动的能力大大降低甚至牵引失败,会导致列车无法准时到站以至于造成地铁运营异常甚至停运、乘客滞留、交通拥堵等问题。牵引系统可靠性是指在规定行车条件下,牵引系统能够在规定行车时间内正常、稳定完成列车牵引制动功能的能力。可靠性评估是保证列车牵引系统安全、可靠运行的重要手段。牵引系统如果在行驶中发生某部件或子系统性能降低,而在维修过程中又没有对该部件或子系统进行详细检测,将增大牵引系统运行风险,造成不必要的经济损失。可靠性预测是提高牵引系统检修水平、优化检修计划的有效手段。若能在牵引系统发生故障之前预估故障可能发生的大致时间,对系统性能仔细检测评估并修正潜在的不可靠性因素,就可以提高列车运行安全性和提高经济效益[10-11]。可靠性评估之后获得的经济效益往往能达到评估费用的3~9倍。
目前,国内对地铁车辆电气系统的检修大多基于经验实施,按照其行驶里程或安全运行时间来制定相关检修计划。维修人员基本按照维修章程对已发生故障的部件进行维修工作,对未发生故障的其他部件多凭经验进行全部宽泛检修。该检修方式灵活性不足,缺乏针对性。牵引系统的检修计划和检修作业的实施,目前仍缺乏完善的科学理论指导。
牵引系统结构如图1所示。
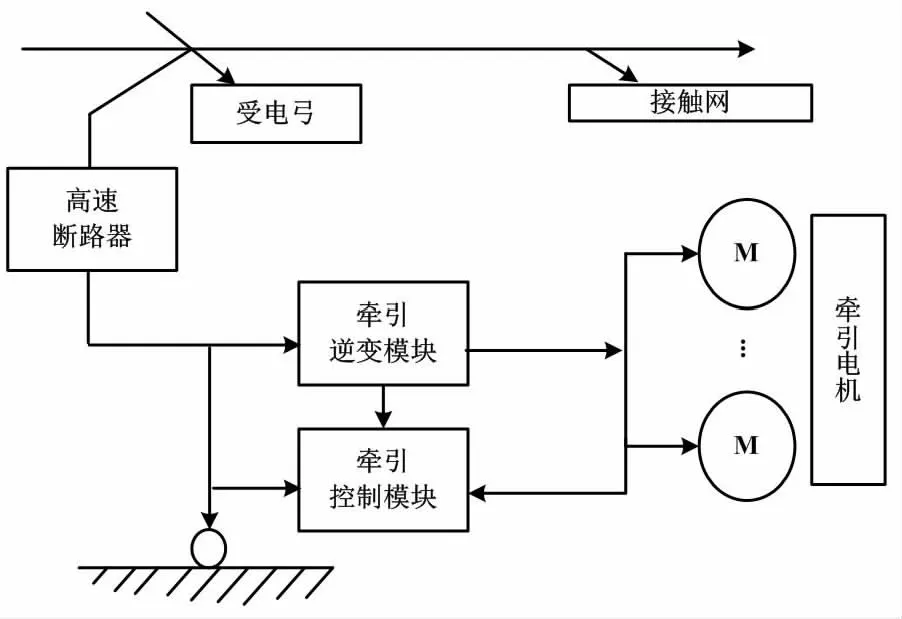
图1 牵引系统结构示意图Fig.1 Traction system structure diagram
由图1可知,牵引系统主要由牵引电机、牵引控制模块、牵引逆变模块、高速断路器、受电弓、接触网等基础部件组成[12]。一般情况下,受电弓起到接通电源的作用。受电弓通过列车线路向高速断路器模块输入直流电,其具体规格选定为1 500 V。牵引控制器会通过应用牵引逆变器完成相应控制信号的输入,将原本属性为直流的电力作调整,继而生成三相交流电,并以此为准牵引电机。需要注意的是,车身与转向架必须借助地刷接地的方式,实现闭环电路的构建。
1.2 常见的故障
牵引系统常见的故障,一般是由过流或过热保护、命令错误等原因导致的。这些故障都是传感器通过系统网络反馈至车载显示器,由列车司机在驾驶过程中发现并作相应处理的。过流故障可以分为直流过流和逆变过流。直流过流是指牵引逆变器中的电流传感器到车门控制单元(domain control unit,DCU) 模块通过车载网络系统向车载显示器反馈时,在LH1电流传感器和DCU模块传输过程中发生电流过流的情况。逆变过流是指牵引逆变器中,LH3和LH4电流传感器、DCU模块、脉冲分配板、绝缘栅双极型晶体管(insulated gate bipolar transistor,IGBT)驱动板、IGBT的逆变过程出现问题,即热保护-牵引逆变器模块内温度继电器信号检测模块内的温度过高,向DCU反馈超温信息,并通过车载网络系统向车载显示屏反馈。电机内设有电机温度传感器,以检测电机工作温度。当传感器检测到牵引电机的工作温度超过180 ℃或者低于50℃时,电机温度传感器则被视为发生故障。命令错误是地铁列车司机操纵列车方向手柄,给出方向指令,网络系统传输指令至牵引逆变器中系统管理控制器(system management controller,SMC) 模块,从而检测到牵引指令出现错误。此时,系统会将反馈信号输出至SMC模块,并通过系统网络显示于车载显示器。
1.3 系统可靠性理论
聚焦可靠性在内容方面表现为五个层面,具体是可靠度、规定条件、使用条件、产品、规定时间。聚焦可靠性存在的指向,往往是服务于产品可靠度。其中,产品是指具体的分析对象。该词汇本身存在着一定宽泛性,涵盖类型众多,可以是牵引系统中的控制开关、IGBT、制动电阻等独立元件,也可以是组件、接收器、子系统等设备,甚至是整个设备。当以地铁牵引系统作为分析对象时,需要关注其现实机理,明确维护策略和人为判断因素。规定是指研究对象的操作条件、工作环境、存储运输、使用维护等。这些控制条件的变化对可靠性有重大影响。规定时间通常用于评估可靠性的时间指标。因为评估主题可靠性是时间调整的定义,所以时间可以是不同的区间,也可以是将另一个指标分配给予时间对应的值,例如服务周期、使用期限等。规定功能是可靠性研究中的重要部分,通常代表指定情况或操作条件下,作为研究对象的产品可以保持继续正常运行而不会出现故障或意外。需要强调的是,规定功能失效并不完全等同于不能工作。在某些情况下,即使产品可以运行,但一些特定参数超出规定范围,该产品也可以被判断为功能失效。可靠度是指所研究对象可靠性的概率,并使用多个概率来表示作为可靠性技术持续发展基础的可靠性。概率的数字表示允许量,用于比较和评估产品或设备系统的可靠性,并确保对这种可靠性的质量控制。
1.4 可靠性定义参量
牵引系统按是否具有修复功能,可以分为两类。对于有修复功能的系统而言,在出现故障或异常时,系统借助一定的干预手段介入与修理,是能够实现其功能完全或部分恢复的。对于没有修复功能的系统而言,则是无法通过干预再次恢复功能的。对于牵引系统而言,其大部分是有修复功能的。
可靠度的定义如式(1)所示。
R(t)=P(T≥t),∝>t>0
(1)
式中:R(t)为时间函数;t为指定的某一时刻;T为随机量;
P为部件正常工作的概率。
与之相对的,不可靠度的定义如式(2)所示。
F(t)=1-R(t)
(2)
系统发生故障的概率可以用故障率表示。故障率的定义如式(3)所示。
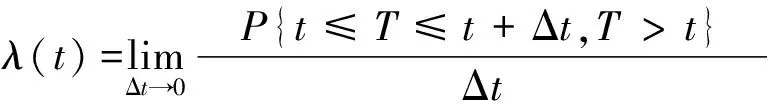
(3)
聚焦修复率指的是在一定时间范围内,故障问题顺利恢复正常的可能性。该指标可以描述故障或组件的修复难度。修复率如式(4)所示。
A(t)=A
(4)
式中:A(t)为修复概率;
A为故障率。
平均无故障工作时间(mean time bewteen failure,MTBF)表示系统、组件从出现故障到再一次投切到运行所耗费的时间均值,也被界定为平均寿命,在本文中被记作B。其可以用式(5)表示。
(5)
式中:θ为平均寿命;
N为样本总量;
ni为第i个部件故障;
tij为第i个部件从第(j-1)次故障到第j次故障的工作时间。
平均维修时间(mean time to repair,MTTR)在本文中被记作C,如式(6)所示。
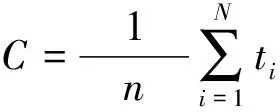
(6)
式中:n为样本;ti为故障时间。
1.5 基于马尔可夫的可靠性预测系统
俄国数学家马尔可夫提出马尔可夫模型,并定义了马尔可夫过程。马尔可夫过程中,下一个状态仅取决于现在状态而与以往的状态无关,即无记忆性。一般采用状态转移图的方法构建马尔可夫模型。根据牵引系统的层次分析模型,本文将地铁牵引系统划分为五个子系统,分别为受电弓模块、高速断路器模块、牵引逆变模块、牵引电机模块和牵引控制模块。使用层次分析法分析地铁牵引系统时,牵引系统中每个模块的组件都非常复杂,且相互关联。因此,使用层次分析法评估地铁牵引系统的可靠性所需时间较长。系统可靠性如图2所示。

图2 系统可靠性框图Fig.2 System reliability block diagram
本文在马尔可夫的可靠性预测系统的基础上提出了基于马尔可夫奖励过程的牵引系统可靠性评估。轨道列车牵引系统分层结构如图3所示。
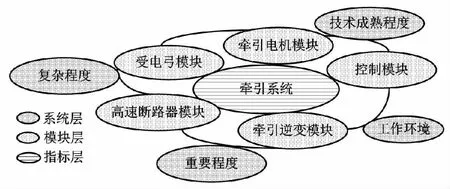
图3 轨道列车牵引系统分层结构Fig.3 Layered structure of rail trains traction system
轨道列车牵引系统分为系统层、模块层以及指标层三层。系统层用于表达系统状态。模块层为系统各模块的状态评估。指标层考虑不同模块的组成特性、运行环境等确定评价指标。
马尔可夫法采用指数估值法的最大边沿原理法确定总权重,简单、直观、方便。估值使用式(7)计算。
(7)
式中:m为评价指标的最大数量;
a为综合权重;
b为权重。
在面向对象作评估分析时,需要重点关注衰减系数以及补偿系数。衰减系数又称衰减常数,是传播系数的实数部分。它包括经典吸收和分子吸收两部分。经典吸收是由于空气的粘滞性、热传导效应以及空气分子转动等所产生的声能耗散,大小与声波频率的平方成正比例,并且与空气温度和气压有关。在对系统进行价值评估时,必须确定不同状态的奖励系数以及衰减系数。奖励系数表示某系统在某状态下的奖励,具体指某一时刻处在某状态下的某系统在下一个时刻能获得的奖励期望。衰减系数定义为未来奖励在当前时刻下的价值比例。若衰减系数接近0,则表明本次为“近视”性评估,衰减系数愈靠近1,则表明偏重考虑远期的利益。分别设衰减系数为0.2、0.5、0.7[13-15],并分别对应从短期、中期、长期的角度评估牵引系统可靠性。这里定义不同时期指在一定安全裕度下,从安全度和经济利益两个方面来评判不同衰减系数对应的时期。短期角度为考虑系统安全度远多于其运维产生的经济利益。中期角度为考虑安全度与其运维的经济利益的程度相当。长期角度则指更多地考虑其经济利益。
2.1 受电弓模块
受电弓模块的作用是从接触网中得到充分的电能。其需要布置在列车顶部。对于列车而言,受电弓模块是极为关键的受流设备。关注其可靠性层面的分析,有助于切实保障其安全性。受电弓模块的可靠性对比如图4所示。
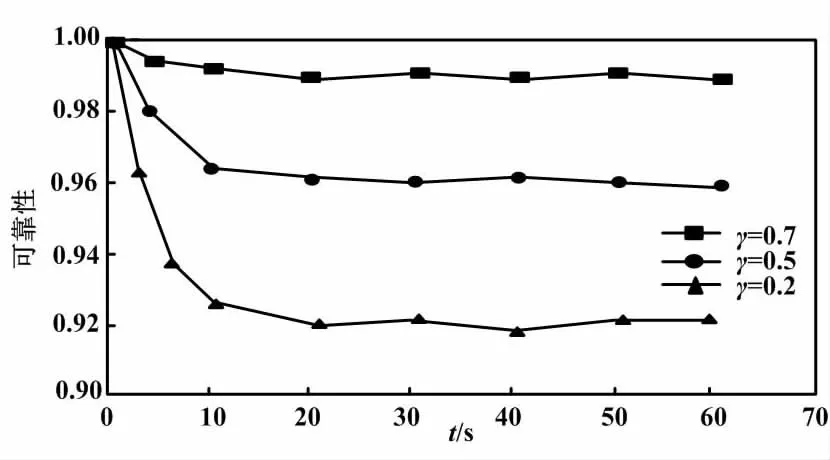
图4 受电弓模块的可靠性对比图Fig.4 Reliability comparison diagram of pantograph module
由图4可知,各个时间段内受电弓模块可靠性的总体下降幅度相同,但下降速度和稳态逼近值不同。考虑到短期收益,受电弓模块可用性下降速率是极为鲜明的,趋近于0.92。关注长期性,其可用性会随之下降,接近0.99。关注中期运作,此时下降速率处于中间位置,稳态可靠性趋于0.96。本研究将安全放在首位并关注短期收益的可靠性曲线,将其作为可靠性维护周期的基线曲线。研究时,根据马尔可夫过程的有条件维修,定义预防维修阈值,并计算每月装配故障数据的最佳稳定维修期。
2.2 高速断路器模块
高速断路器模块对于列车而言是一个具体的高压模块。一旦系统中出现了短路或其他电气问题,该模块便会快速反应,及时关闭牵引逆变器等用电机构,以免波及到其他设备或引起设备温度过高而烧坏设备。可靠性评估有助于提高列车的可靠性和子系统中其他设备的性能。高速断路器模块可靠性对比如图5所示。
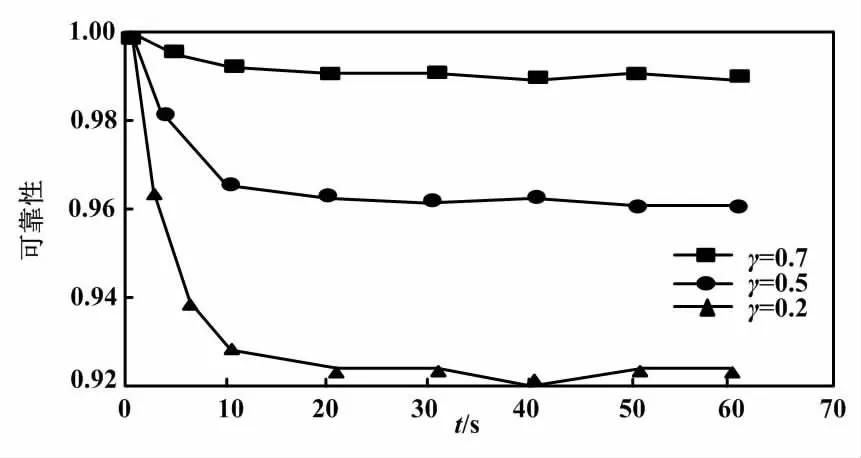
图5 高速断路器模块可靠性对比图Fig.5 Reliability comparison diagram of circuit breaker module
由图5可知,各时间点高速断路器模块可靠性呈整体下降趋势,但其衰减率和稳态逼近值不同。考虑到短期收益,高速断路器模块可靠性下降速度最快,最终趋于0.83。考虑到长期收益,可靠性下降表现为最缓慢,最终结果具体表现为0.92。关注中期收益,其稳态可靠性趋于0.89。本研究使用将安全放在首位并关注短期收益的可靠性曲线作为可靠性维护周期的基线曲线。根据马尔可夫过程进行状态维护,定义0.95为t=3.5时所对应的预防性维护阈值,计算月度故障数据调整需要3~5个月的最大可靠期。
2.3 牵引逆变模块
牵引逆变器的关键任务是面向牵引电机,提供充分的三相交流电。地铁车辆的列车牵引系统降低了能耗。
牵引逆变模块可靠性对比如图6所示。由图6可知,牵引逆变模块的可靠性呈整体下降趋势,但其下降率和稳态方法是不同的。考虑到短期收益,牵引逆变模块可靠性下降最快,结果表现为0.73。关注长期收益,其结果会达到0.81。关注中期收益,下降率处于中间,稳态可靠性趋于0.77。本研究保持安全第一的原则,以短期收益为导向的正常运行时间曲线作为可靠性维护周期的基线曲线。根据马尔可夫过程状态维护,将0.95设为t=0.9时所对应的预防性维护阈值,以0.9个月计算月度不合格数据并进行检修。
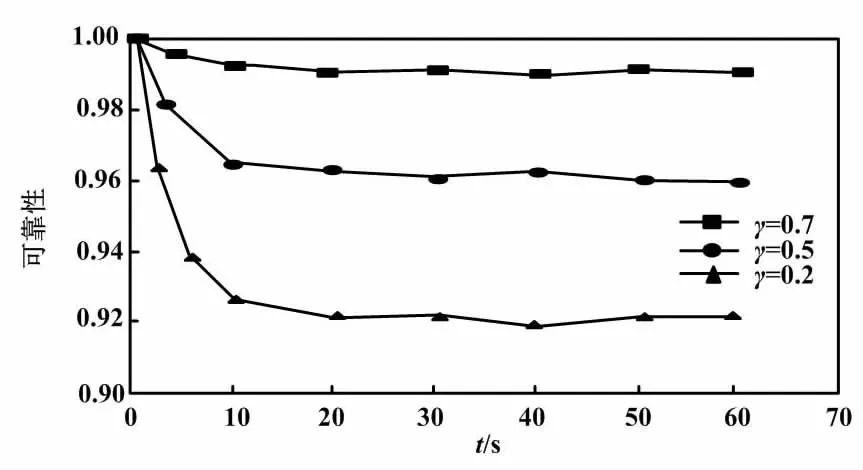
图6 牵引逆变模块可靠性对比图Fig.6 Reliability comparison diagram of traction inverter module
2.4 牵引电机模块
对于地铁而言,牵引电机是极为关键的,直接关联着列车的移动性能。针对该模块,也必须给予充分的可靠性探索。牵引电机模块可靠性对比如图7所示。
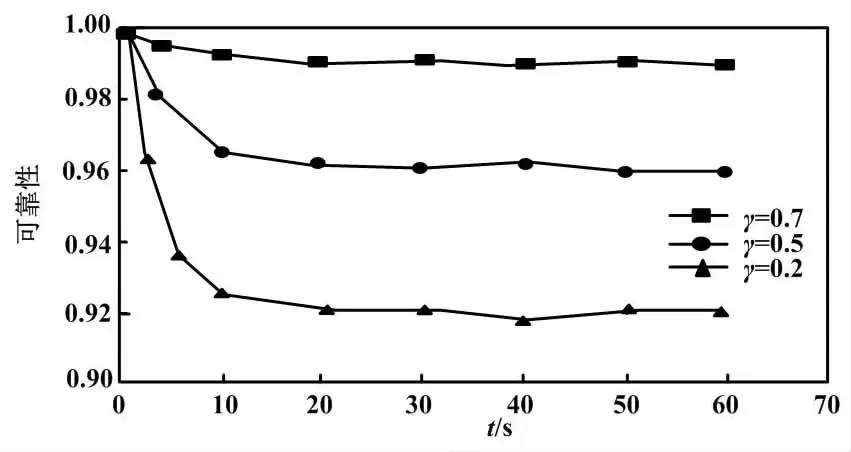
图7 牵引电机模块可靠性对比图Fig.7 Reliability comparison diagram of traction motor module
由图7可知,各时间点主电机模块可靠性呈整体下降趋势,但其下降率和稳态逼近值是不同的。考虑到短期收益,牵引电机模块可靠性下降是最快的,结果表现为0.84。关注长期收益,可靠性呈下降态势,速度最慢,最终达到0.98。考虑中期收益,可靠性下降处于中间,稳态可靠性趋于0.92。本研究以安全为首要考虑,以短期收益为导向的可靠性曲线作为可靠性维护周期的基线曲线。根据基于马尔可夫过程的状态维护,在计算t=1.6所对应的预防性维护阈值和月度不合格数据时,可靠性维护的最佳周期为1.6个月。
2.5 牵引控制模块
对于牵引系统本身而言,其中的牵引控制模块承载着指令输入、参数界定等关键任务,包括相关信号的转换、脉冲参数的设置等,以控制牵引马达。评估其可靠性有助于降低列车控制故障率并提高列车运行性能。牵引控制模块可靠性对比如图8所示。由图8可知,牵引控制模块可靠性在不同时间段的总体减少量相同,但减少率和稳态逼近值不同。具有短期收益的可靠性下降最快,最终达到0.83。具有长期收益的可靠性下降最慢,最终达到0.93。关注中稳态可靠性趋于0.89。其预防性维护阈值为0.95。本研究有条件维护马尔可夫过程,使用关注短期收益的可靠性曲线作为可靠性维护周期的参考曲线,以安全为首要考虑。设置t=1.4。在计算装配月份的故障数据时,1.4个月是最可靠的检验周期。
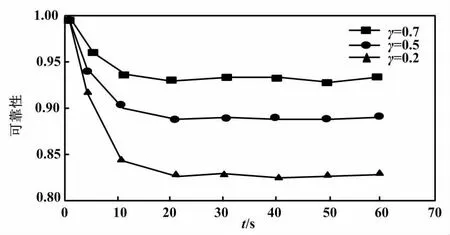
图8 牵引控制模块可靠性对比图Fig.8 Reliability comparison diagram of traction control module
2.6 牵引系统可靠性评估
牵引系统可靠性评估曲线如图9所示。
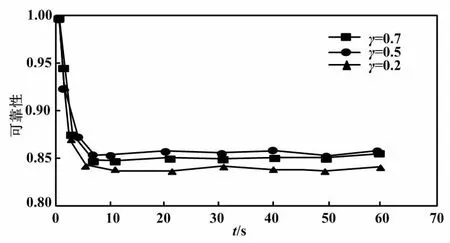
图9 牵引系统可靠性评估曲线Fig.9 Reliability evaluation curves of traction system
由图9可知,牵引系统在不同时间具有相同的整体下降趋势,但其降速和稳态接近的值不同。所有牵引系统的稳态方法的短期收益可用性下降速度最快,低于每个子系统模块的成本。考虑到长期收益,可靠性最终很可能达到0.59、趋近于0.63。考虑到中期收益,可靠性下降率介于两者之间,稳定可靠性趋近于0.62。本研究秉持安全第一的原则,以强调短期收益的可靠性曲线作为可靠性维修周期的参考曲线。根据状态维修流程设定t=0.4时所对应的预防性维护阈值,计算每个月份的误差数据时,以0.4个月作为最佳可靠性维护期。
本文以地铁线路的主交流电模型铁路牵引系统作为标准,评估轨道列车的牵引系统可靠性,对系统常见的故障形式和可能的故障原因展开分析,并利用马尔可夫奖励过程来提升牵引系统的可靠性。相关子模块的存在随着时间的推移在各种阻尼因素下发生变化。本文通过对牵引系统水平的评值,首先确定了评价牵引系统可靠性的指标,并计算整个系统中各子系统模块的全局权重;
然后利用马尔可夫模型对系统的可靠性进行评价;
最后根据系统可靠性评估模型和评估结果,提供合理的维护周期。该模型对地铁列车牵引系统的可靠性评估及制定维修维护策略具有重要的参考价值。