陈伟先, 欧孝夺, 吴昱芳, 江 杰
(1.南宁工程咨询集团有限公司, 南宁 530201; 2.广西大学 土木建筑工程学院, 南宁 530004)
公路隧道施工过程中存在着不可预见的因素和巨大的安全风险。由于其周期长、 对围岩扰动大, 因而难以实现高效、 安全的施工。坍塌是隧道施工最常见的事故之一, 在隧道施工事故中占比35%[1]。坍塌事故不仅威胁施工人员的生命安全, 还会造成经济损失和工期延误。在各类地质灾害事故中, 坍塌造成的人员伤亡高达51.26%[2]。因此, 对隧道施工进行风险评估具有重要意义。
目前, 对隧道施工风险的评估提出了各种各样的方法,主要有层次分析法[3]、 模糊综合评价法[4]、 故障树分析[5]、 云模型[6]和D-S证据理论[7]等。贝叶斯网络作为隧道风险评估最常见的方法之一, 在处理复杂逻辑问题时, 能兼顾专家经验和实时监测数据, 构建可正向和反向推理的可视化网络, 并通过自主学习对新输入的证据进行数据更新, 保证评估结果的时效性, 在隧道坍塌风险评估中具有明显优势。贝叶斯网络已经被应用于地铁隧道工程[8]和基坑围护[9]风险评估当中:
周建国等[10]提出了基于模糊多态贝叶斯网络的地铁运营隧道结构风险评估方法;
郭发蔚等[11]运用贝叶斯网络对隧道施工风险自然概率进行计算, 并结合模糊理论对其进行风险评级。
贝叶斯网络节点的状态概率确定是推理过程的重要步骤。由于坍塌风险因素往往具有不确定性, 风险因素构成的贝叶斯节点状态需要多态的逻辑表达。郑来等[12]基于T-S模糊故障树和贝叶斯网络的融合, 用梯形隶属函数来描述底事件发生概率和故障程度, 克服了传统故障树不能考虑事件中间故障状态对系统影响的问题。模糊数学和灰色系统理论为贝叶斯不确定性分析提供了重要依据, 被广泛应用于各个领域当中。利用模糊数学和模糊逻辑, 能很好地处理各种不确定性问题。隶属函数的确定, 无论是从理论上还是实践上, 都是模糊数学及其应用的关键问题。灰色系统理论是关于信息不完全或者不确定的系统控制理论, 在解决风险状态不确定性的问题上, 能对梯形隶属函数和贝叶斯条件概率进行模糊化处理。灰色理论在隧道变形预测[13]和洞口塌方时空预测[14]已有运用。
然而, 如何把贝叶斯网络、 模糊数学和灰色系统理论有机地结合起来, 充分发挥各种方法在隧道施工安全风险评估上的优势, 这点在目前的研究成果中还较少见。鉴于此, 本文将灰色系统理论引入贝叶斯网络推理当中, 提出一种灰色模糊贝叶斯网络的隧道施工坍塌风险评估方法。基于传统贝叶斯推理方法和灰色系统理论, 把贝叶斯网络叶节点风险状态概率、 根节点重要度等特征参量拓展为灰色模糊概率、 灰色模糊状态重要度、 灰色模糊关键重要度等。以某公路隧道坍塌风险评估为例, 预测坍塌风险状态的概率并找出关键致险因素, 为相关的风险评估和管理提供参考。
贝叶斯网络(Bayesian network, BN)[15]是一个由节点和条件概率表(conditional probability table, CPT)组成的有向无环图(directed acyclic graph, DAG), 可以进行正向和反向推理, 如图1所示。DAG由节点和有向边构成, 节点表示坍塌风险状态变量, 包含父节点和子节点, 有向边由父节点指向子节点。节点之间的逻辑关系由CPT确定。
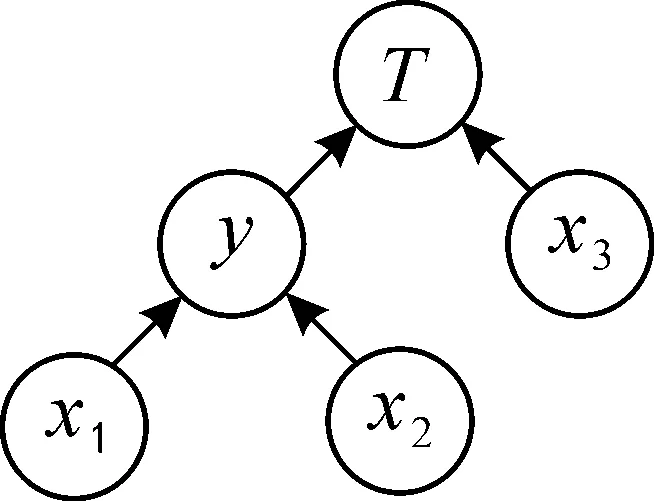
图1 贝叶斯网络有向无环图
隶属函数是用于表征模糊集合的数学工具, 具有不分明性。本文采用梯形隶属函数来描述某时刻隧道坍塌风险状态的模糊不确定性。
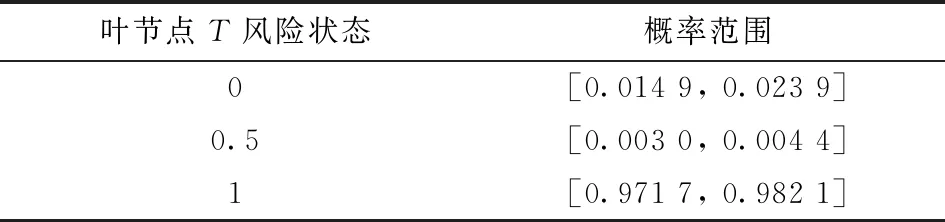
灰色系统理论是关于信息不完全或者不确定的系统控制理论, “灰数”是灰色系统的基本单元, 它采用区间而不是一个精确值来描述不确定性。本文采用区间灰数⊗i∈[ai,bi],其中i=1, 2, …,n, 表示模糊程度; 因此, 构建灰色模糊的梯形隶属函数用于描述隧道坍塌风险状态的不确定性, 结合含区间灰数⊗的条件概率, 对风险状态发生概率进行贝叶斯推理。灰色模糊贝叶斯网络评估方法步骤如图2所示。 图2 灰色模糊贝叶斯网络评估方法流程图 在隧道坍塌风险评估问题上, 由于隧道施工具有地质条件复杂、 施工环境恶劣和隐蔽性高等特点, 往往具有不可预见性和模糊性。因此, 许多风险因素的状态需要多种状态的逻辑表达。本文针对贝叶斯网络节点的不同状态, 构建梯形隶属函数来表征贝叶斯节点的坍塌风险状态, 如图3所示, 并表示为 μ(x)=(m0,sL,sR,fL,fR), (1) 式中:m0为模糊数支撑集的中心;sL和sR为左右支撑半径;fL和fR为左右模糊区, 如图3所示。当sL=sR=0时, 梯形隶属函数变为三角隶属函数; 当fL=fR=0时, 模糊数变为确定数。 图3 梯形隶属函数 (2) 建立灰色模糊梯形隶属函数见图4。其中, ⊗μk(k=1, 2, 3, 4)为风险状态隶属度对应的区间灰数。可知, 支撑半径影响着隶属函数的模糊区, 各风险状态的隶属度计算公式见表1。 图4 灰色模糊梯形隶属函数 表1 节点风险状态隶属度 公路隧道在施工过程中存在诸多不确定性, 施工周期长且完成难度大。某个风险因素不能独立引起隧道坍塌事故, 但风险因素之间的联系密切相关。如掌子面前方的断层破裂带或涌水突泥都可能直接导致隧道坍塌。另外, 暴雨作用下断层破裂带会首先导致开挖面后发生涌水突泥, 由于水或泥浆涌出的持续时间较长, 可能进一步导致隧道坍塌。在这一点上, 断层破裂带和涌水突泥这两个因素之间不是并列的关系, 而是诱导的关系[16]。因此, 风险因素之间的逻辑关系往往带有很大的灰色信息, 如果简单地用精确值来表示风险因素节点之间的关系会给结果带来误差。为了精确描述风险因素与坍塌事故之间的逻辑关系, 用区间灰数⊗来表示贝叶斯网络节点的条件概率。对于任一包含n个m种状态节点的灰色模糊贝叶斯网络CPT如表2所示。其中, 每行代表当父节点不同风险状态时, 子节点为某风险状态的条件概率, 如第一行P(y=i|x1=0,x2=0, …,xn=0)=⊗1, 1, …, i表示节点x1、x2、 …、xn风险状态都为0时, 节点y风险状态i的概率为区间灰数⊗1, 1, …, i, ⊗1, 1, …, i∈[0, 1], 且满足⊗1, 1, …, 1+…+⊗1, 1, …, i+…+⊗1, 1, …, m=1。 表2 灰色模糊贝叶斯网络CPT 贝叶斯网络推理是构建贝叶斯网络的最终目的, 利用贝叶斯的双向推理能力, 可对隧道坍塌风险评估贝叶斯网络叶节点风险状态概率、 根节点重要度等特征参量进行分析。在传统贝叶斯网络推理的基础上, 结合灰色系统理论, 把系统特征参量拓展为灰色模糊概率、 灰色模糊状态重要度、 灰色模糊关键重要度等。 (3) (4) (5) P⊗(T=Tq|xi=0)], (6) (7) 2.3.3 评估模型特征 参量求解: 把区间灰数运用在描述节点风险状态模糊程度和表征风险因素与坍塌事故之间的逻辑关系时, 所得到的评估模型特征参量, 将是一系列包含灰色模糊隶属函数和条件概率的区间灰数映射关系集。为了得到评估模型特征参量的最终取值范围, 构建参数规划模型: max(min)f(⊗1,⊗2,…,⊗n), (8) 某隧道为双线分离式隧道, 全长782 m, 最大埋深131 m, 其中Ⅴ级围岩段长367 m, Ⅳ级围岩段长415 m。主要为黑云母花岗岩侵入构造, 侵入接触带位于线路右侧30~100 m部位, 侵入接触带平面延伸方向与线路基本一致。洞身为中风化花岗岩, 受花岗岩侵入带影响, 岩体较破碎, 呈块状镶嵌结构或镶嵌破碎结构, 节理裂隙发育, 存在坍塌危险。因此, 有必要对该隧道进行坍塌可能性评价。 《公路桥梁和隧道工程施工安全风险评估指南》(2011)在选择隧道施工安全风险评估指标时, 考虑了地质条件、 建设规模、 气候与地形条件等评估指标。然而, 设计因素、 施工技术以及施工管理引起的风险也不容小觑。本文对一定工程数量的隧道塌方和大变形实例进行统计分析, 把影响隧道塌方的主要因素归纳为四大类: 地质条件、 设计因素、 施工因素和管理因素。以隧道坍塌风险为贝叶斯网络的叶节点T, 以地质条件、 设计因素、 施工因素和管理因素为中间节点y1、y2、y3、y4, 以四大因素对应的风险因素为根节点x1、x2、 …、x14, 构造隧道坍塌风险为贝叶斯网络DAG, 如图5所示。 图5 隧道坍塌风险贝叶斯网络模型 隧道坍塌风险贝叶斯网络节点所对应的风险因素或风险事件见表3。根据公路隧道坍塌风险模式和机理分析, 将风险因素和隧道坍塌按风险状态设为低度风险、 中度风险和高度风险, 并用集合{0, 0.5, 1}表示。以节点y1为算例, 根据历史数据、 工程实际和专家经验, 构造节点y1灰色模糊贝叶斯CPT和灰色模糊隶属度, 如表4、 5所示。由贝叶斯网络节点的逻辑关系可知, 多态性系统子节点的发生是由至少1个有效的父节点引起的。在表4中,节点x1=0,x2=0.5,x3=0.5时, 即围岩等级状态为低度风险, 富水性和不利地质风险状态为中度风险, 此时认为地质条件风险状态为中度风险的概率为0.35, 风险状态为低度风险和高度风险的概率尚不能明确, 因此采用区间灰数表示模糊不确定性。在表5中, 结合工程项目实际情况, 该隧道区段地下水以基岩裂隙水为主, 基岩裂隙水主要赋存于基岩强、 中风化层, 其中中风化岩体相对较完整, 透水性和富水性一般。因此, 认为富水性的风险状态为高度风险的概率很小(为0.05), 而低度和中度风险采用区间灰数来描述。 表3 隧道坍塌风险的贝叶斯网络节点 表4 节点y1灰色模糊贝叶斯条件概率 表5 节点y1灰色模糊隶属度 根据式(8), 构造节点y1处于低度风险的特征参数规划模型为 max(min)P⊗(y1=0); (9) 式中: 0.44≤⊗1≤0.59, 0.08≤⊗2≤0.21, 0.39≤⊗3≤0.57, 0.16≤⊗4≤0.30, 0.22≤⊗5≤0.34, 0.04≤⊗6≤0.17, 0.37≤⊗7≤0.52, 0.05≤⊗8≤0.18, 0.37≤⊗9≤0.51, 0.36≤⊗10≤0.53。结合式(3), 采用全局优化算法, 计算得到 即y1处于低度风险的概率取值范围是[0.187 4, 0.205 8]。同理,y1处于中度风险和高度风险的概率范围分别为[0.040 7, 0.041 8]和[0.753 5, 0.770 8]。按照同样的方法,可以构造y2、y3、y4和T的灰色模糊贝叶斯CPT和灰色模糊隶属度。计算得到叶节点处于不同风险状态的概率取值范围见表6。根据区间灰数大小比较规则可知,P(T=1)>P(T=0)>P(T=0.5), 即隧道坍塌处于高度风险状态的概率大于低度和中度风险状态的概率。 表6 叶节点T各风险状态的概率取值范围 本文采用贝叶斯网络推理软件Netica计算根节点后验概率和灰色模糊重要度, 结果如表7所示。计算根节点的后验概率, 可以根据后验概率的排序检测最可能的致险因素。当隧道发生中度坍塌, 检测影响因素处于中度风险状态时, 后验概率结果为P(x1=0.5|T=0.5)>P(x7=0.5|T=0.5)>P(x10=0.5|T=0.5)>P(x9=0.5|T=0.5)>…, 因此可按照围岩等级→开挖方法→初期支护→开挖跨度…的顺序进行检测; 当隧道发生严重坍塌, 检测影响因素处于高度风险状态时, 后验概率结果为P(x1=1|T=1)>P(x10=1|T=1)>P(x8=1|T=1)>P(x12=1|T=1)>…, 因此可按照围岩等级→初期支护→超前支护→监控量测……的顺序进行检测。 表7 根节点后验概率和灰色模糊重要度 为验证所提方法在隧道坍塌风险评估中的可行性, 基于图1模型, 采用文献[17]的T-S模糊故障树方法计算隧道坍塌的风险概率, 并与本文结果进行对比, 两种方法预测的隧道坍塌风险状态概率基本相同(表8)。重要度计算结果对比见图6, 灰色模糊贝叶斯方法得到的结果包含文献[17]方法计算得出的结果, 验证了本文方法的有效性。 图6 根节点灰色模糊重要度分布 表8 叶节点T风险概率的结果对比 在工程实际中, 隧道洞身段存在黑云母花岗岩侵入构造以及地层角度不整合接触带, 周围岩体节理裂隙发育, 岩体破碎。洞身地下水位高于路面设计标高, 存在坍塌危险。开挖后发生隧道拱顶塌方事故, 并出现裂隙空腔, 临时钢拱架被落石压至变形, 计算结果与实际状态吻合。 (1)将灰色系统理论中的区间灰数引入贝叶斯模型当中, 构建了一种灰色模糊贝叶斯网络模型。该模型用包含区间灰数的模糊隶属度描述节点的风险状态, 用区间灰数表示节点之间的逻辑不确定性, 更能表现隧道坍塌风险的复杂性, 同时提高了贝叶斯网络处理不确定数据的推理能力。 (2)构建一种评估模型特征参量的参数规划模型, 用于确定区间灰数的最终取值范围。基于全局优化算法和贝叶斯网络推理, 能够推断出隧道坍塌风险的概率和节点的重要度信息, 为判断风险发生可能性和确定关键致险因素提供决策支持。 (3)本文利用灰色模糊贝叶斯方法对某隧道进行坍塌可能性评价, 结果表明, 隧道坍塌处于高度风险状态的概率要远大于中度风险和低度风险的概率。结算结果与T-S模糊故障树方法所得结果接近, 并与实际开挖状态吻合, 验证了本文方法的有效性, 为隧道坍塌风险评估提供理论指导。
ai、bi为区间灰数⊗的上、 下界, 且满足ai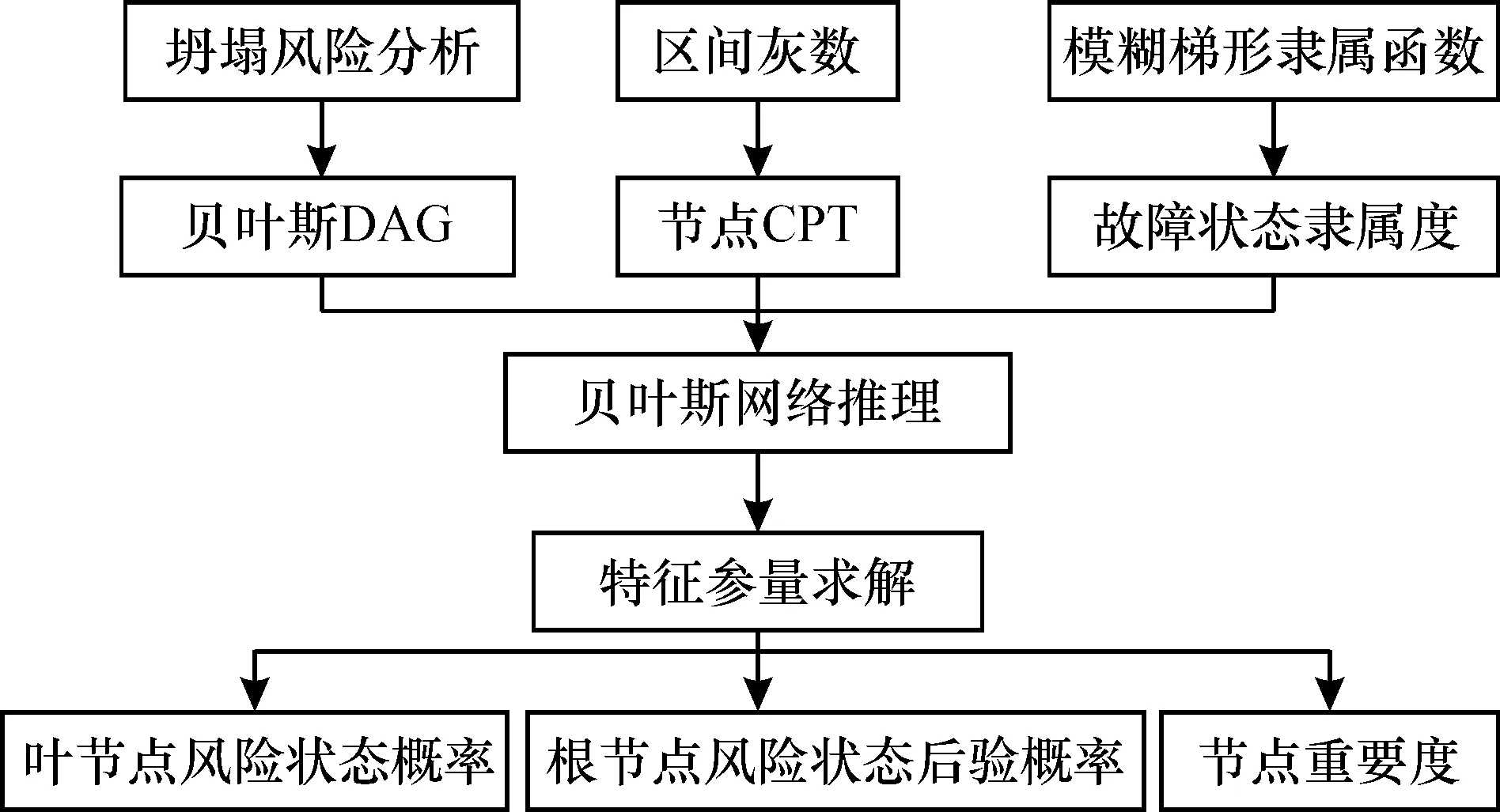
2.1 灰色模糊贝叶斯网络节点的故障状态描述




2.2 灰色模糊贝叶斯网络的CPT

2.3 灰色模糊贝叶斯网络推理分析

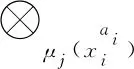
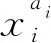

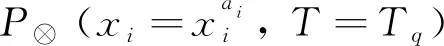

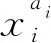



3.1 工程背景
3.2 灰色模糊贝叶斯隧道坍塌风险评估





3.3 结果对比分析及验证

